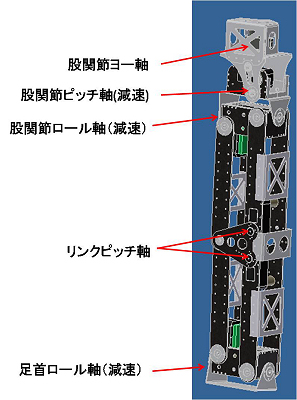
減速機構

　ロボットが大型化してくると、非常に大きなトルクが必要に成ってくる。そこで、鉄人５号では、サーボモーターの減速機構を取り入れた。ただし、減速機構を入れると、動作スピードが遅くなる。そこで、比較的速度が遅くても構わない軸のみに、減速機構を取り入れている。５号では、並行リンク機構を取り入れているため、リンクピッチ軸は速度が必要となる。一方、ロール軸２か所と、股関節のピッチ軸は比較的低速度でも構わない。そこで、この３軸に減速機構を取り入れることとした。
　減速の方法はいくつかあるが、ここでは長穴式を用いた。
　

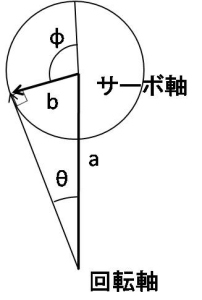
長穴式の減速機構について、理論解析を行った。今、サーボ軸の中心と減速機構の回転軸中心との距離をa、サーボ軸の周りのアーム回転半径をbとする。すると、下のような図を描くことができる。

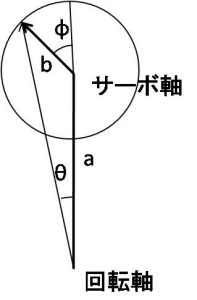
　この図から、回転角θ=atan(b*sin(φ)./(a+b*cos(φ)))となることが分かる。そこで、aとbの比を変えて、サーボの回転と減速機の回転角度にどのような関係があるかを計算してみた。以下が、回転角と、減速比率の計算結果である。比率が大きくなるほど、減速は大きくなる。また、中央から端に行くに従い、減速比率は大きくなる。a=bの場合、減速比1:2で半分の角度になりサーボの回転と減速角度は比例するが、それ以外の場合は非線形な変化を示す。もう一つわかることは、アームはサーボ軸の内側より外側にした方が、減速比は大きく取れ、減速比の非線形性が少ないということである。
　

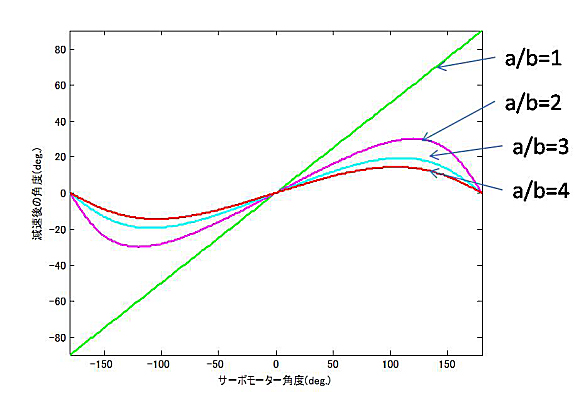サーボモーター角度と減速後の角度

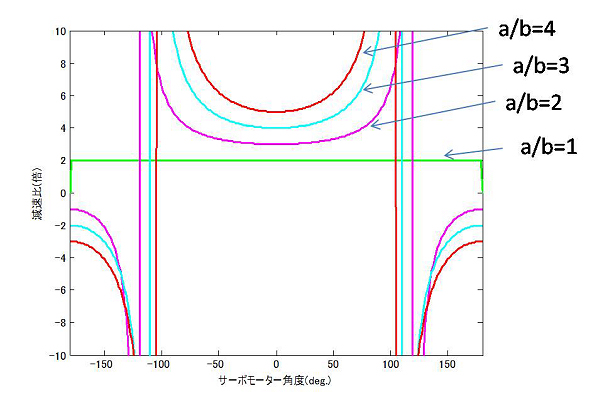サーボモーター角度と減速比

　φ=θ=0のときの、a/bと減速比の関係を計算した。減速比は、a/b+１に比例する。これは、サーボと減速機の軸距離aが大きくなるほど、またサーボアームが短いほど、減速は大きくなることを意味する。

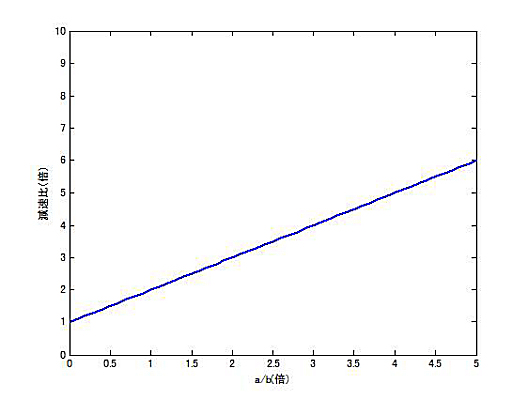a/bと減速比(φ=θ=0)

減速が大きくなれば、可動範囲は狭くなる。減速機の最大角度は、図のようにアームが描く円と減速機の軸からアーム先端までの直線が接する時として計算できる。すなわち、θ=asin(b/a)

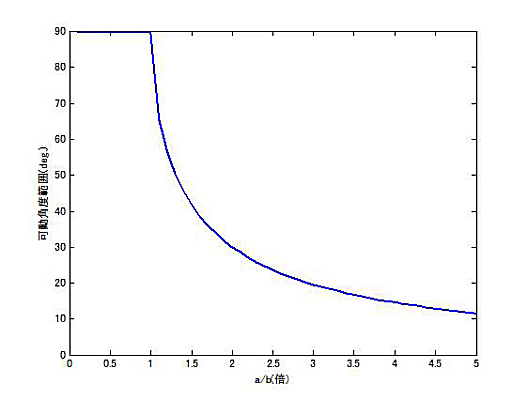a/bと可動角度範囲

　最後に、サーボモータのトルクを２８８ｋｇ・ｃｍとした場合の、減速後のトルクをa/bについて計算した。これは、288×減速比で計算できる。すなわち、
　
　　　　　　　　　　　　減速トルク＝サーボトルク×(1+a/b)
　
　であることがわかる。ただし、これはφ=θ=0度付近であり、角度とともに減速トルクはさらに大きくなる。
　a/b=1で２倍の５７６ｋｇ・ｃｍ、a/b=2.5で１トン・ｃｍ以上のトルクが得られることになる。

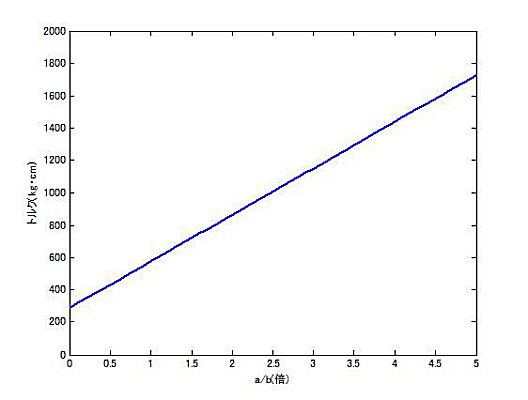a/bとトルク
（サーボトルク２８８ｋｇ・ｃｍ）

　今回は、a/b=1とa/b=2の減速機を使用した。

a/b	トルク（θ=0）（kg・cm）	可動範囲（度）
1	５７６	±90
2	８６４	±30
3	１１５２	±20